Итак, сегодня мы приступаем к решению задачи B15.
Сколько различных решений имеет логическое уравнение
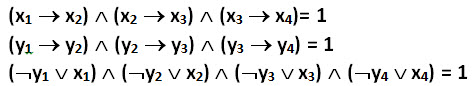
где x1, x2, …, x4 и y1, y2, …, y4 – логические переменные? В ответе не нужно перечислять все различные наборы значений переменных, при которых выполнено данное равенство. В качестве ответа нужно указать количество таких наборов.
Решение:
· Найти решения первого уравнения
· Найти решения второго уравнения
· Найти множество решений первого и второго уравнения
· Из множества решений первого и второго уравнений убрать те, которые не удовлетворяют третьему уравнению
Ищем решения первого уравнения:
Решение первого уравнения можно записать, как битовую цепочку длиной 4 бита. Поскольку импликация (х1 -> x2) будет ложна при х1 = 1 и х2 = 0, то в нашей цепочке не должно быть сочетания «10». Это все нам дает такие решения (других быть не может!!!):
(х1, х2, х3, х4) = 0000 0001 0011 0111
1111
Ищем решения второго уравнения:
Поскольку второе уравнение полностью совпадает с первым, то его решения будут такими же:
(у1, у2, у3, у4) = 0000 0001 0011 0111 1111
Ищем множество решений первого и второго уравнения:
Первые два уравнения не зависят друг от друга, поэтому система из этих двух уравнений будет иметь 25 решений (каждому первому соответствуют 5 разных решений второго, и наоборот, каждому второму соответствуют 5 разных решений первого):
(у1, у2, у3, у4) = 0000 0001 0011 0111 1111
(х1, х2, х3, х4) = 0000 0000 0000 0000 0000
(х1, х2, х3, х4) = 0001 0001 0001 0001 0001
(х1, х2, х3, х4) = 0011 0011 0011 0011 0011
(х1, х2, х3, х4) = 0111 0111 0111 0111 0111
(х1, х2, х3, х4) = 1111 1111 1111 1111 1111
Ищем решения третьего уравнения:
Третье
уравнение можно переписать в виде
Теперь подставляем значения второго уравнения:
Импликация (y1 -> х1) ложна при у1 = 1 и х1 = 0, следовательно, такая комбинация невозможна, таким образом, набору с у1 = 1 соответствует только одно решение, в котором х1 = 1.
Поэтому множество решений «редеет»:
(у1, у2, у3, у4) = 0000 0001 0011 0111 1111
(х1, х2, х3, х4) = 0000 0000 0000 0000
(х1, х2, х3, х4) = 0001 0001 0001 0001
(х1, х2, х3, х4) = 0011 0011 0011 0011
(х1, х2, х3, х4) = 0111 0111 0111 0111
(х1, х2, х3, х4) = 1111 1111 1111 1111 1111
Идем дальше:
Импликация (у2 -> x2) ложна при у2 = 1 и х2 = 0, следовательно, такая комбинация невозможна, таким образом, набору с у2 = 1 соответствует только два решения, в котором х2 = 1.
Множество решений «редеет»:
(у1, у2, у3, у4) = 0000 0001 0011 0111 1111
(х1, х2, х3, х4) = 0000 0000 0000
(х1, х2, х3, х4) = 0001 0001 0001
(х1, х2, х3, х4) = 0011 0011 0011
(х1, х2, х3, х4) = 0111 0111 0111 0111
(х1, х2, х3, х4) = 1111 1111 1111 1111 1111
Аналогично проверяем дальше, в итоге у нас получится такая таблица:
(у1, у2, у3, у4) = 0000 0001 0011 0111 1111
(х1, х2, х3, х4) = 0000
(х1, х2, х3, х4) = 0001 0001
(х1, х2, х3, х4) = 0011 0011 0011
(х1, х2, х3, х4) = 0111 0111 0111 0111
(х1, х2, х3, х4) = 1111 1111 1111 1111 1111
Всего решений: 1+2+3+4+5 = 15.
Ответ: 15.
| Всего комментариев: 1 | ||||||
| ||||||



